新的“余数公式M式”特性引伸
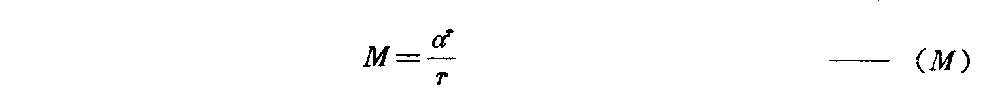













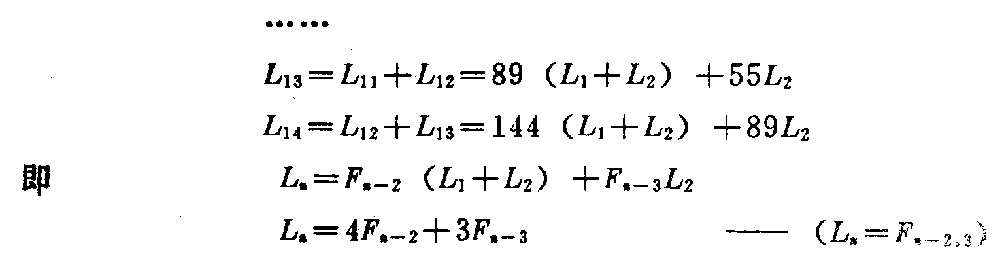
摘自《运动论》400—417页
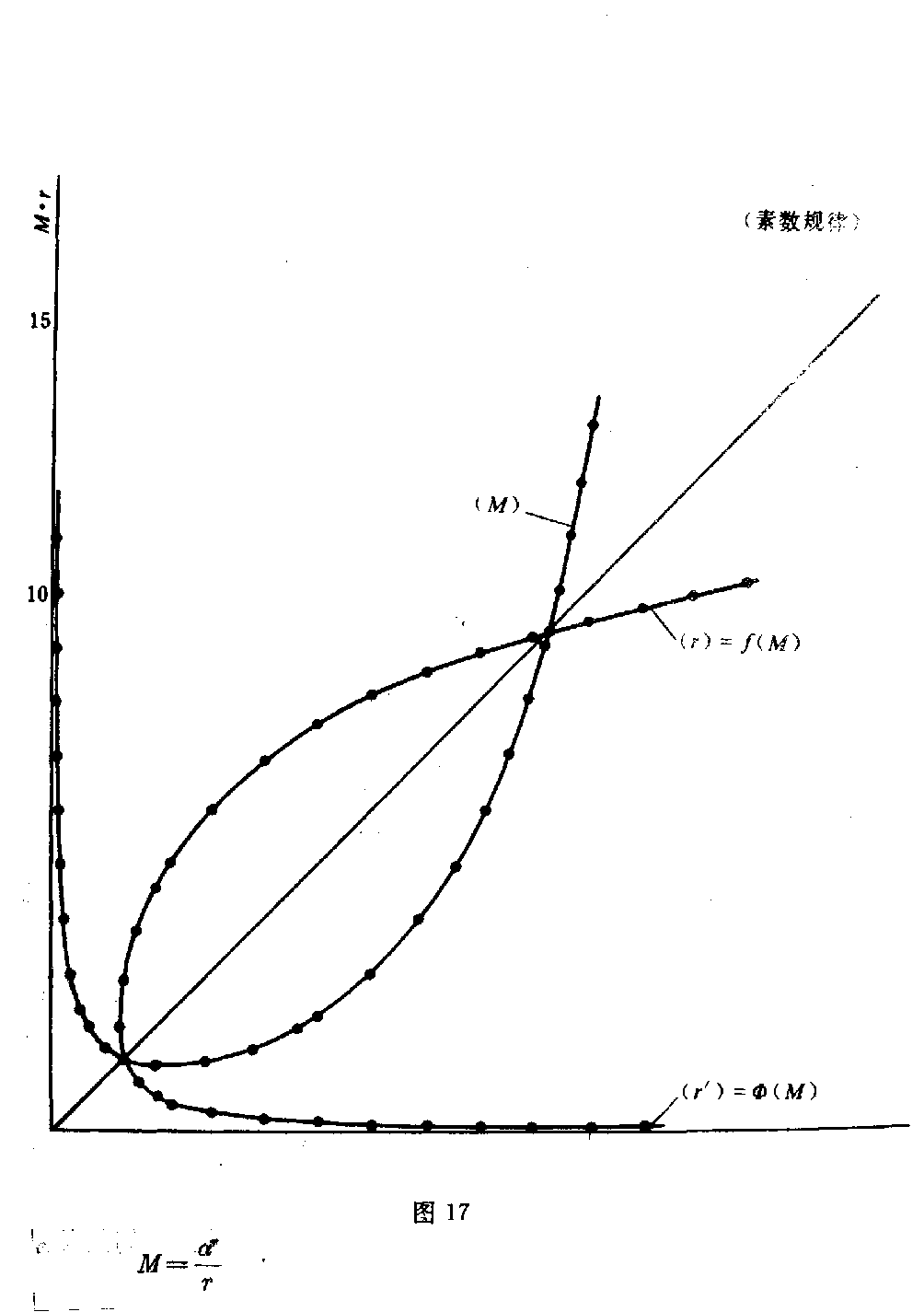
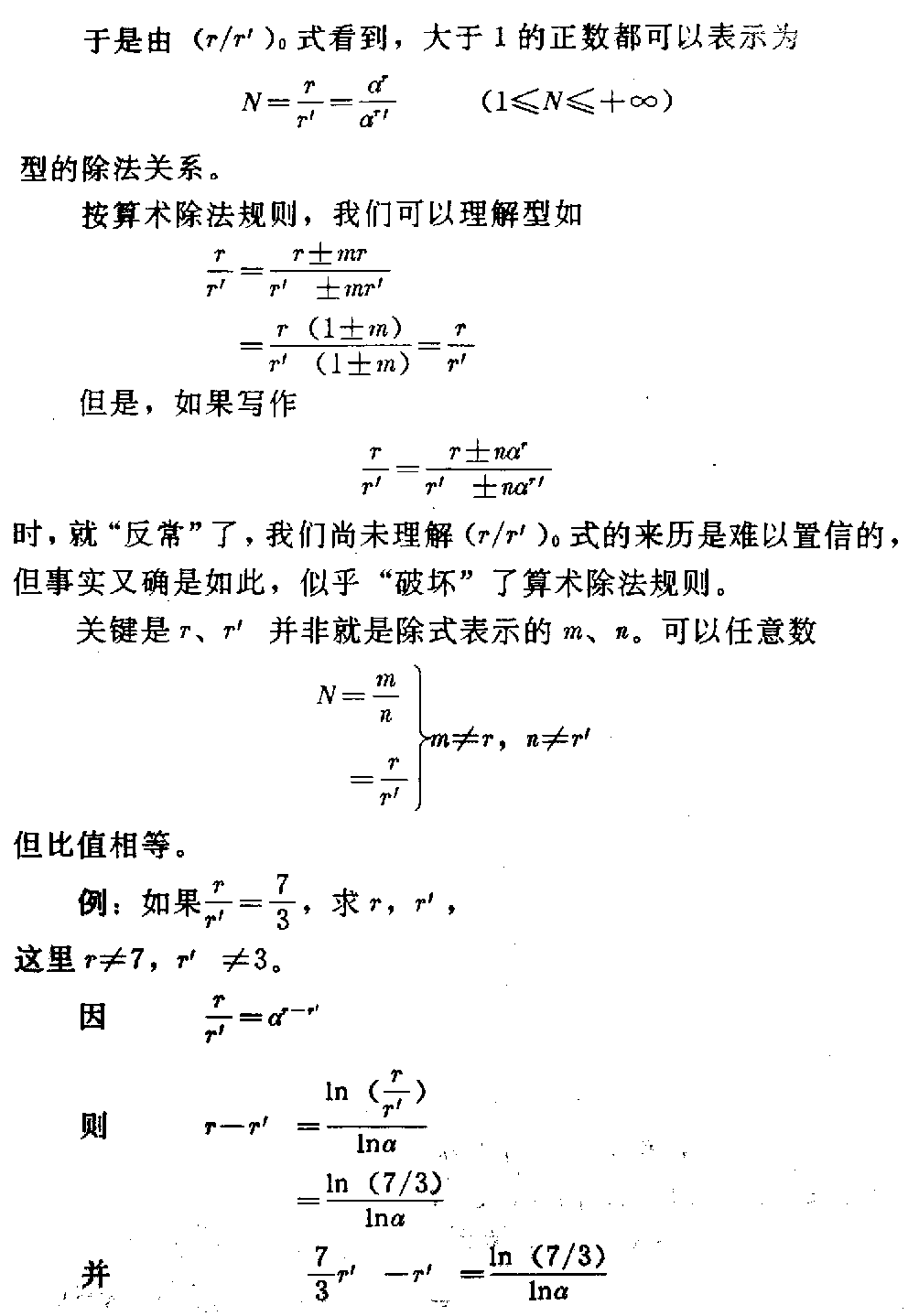
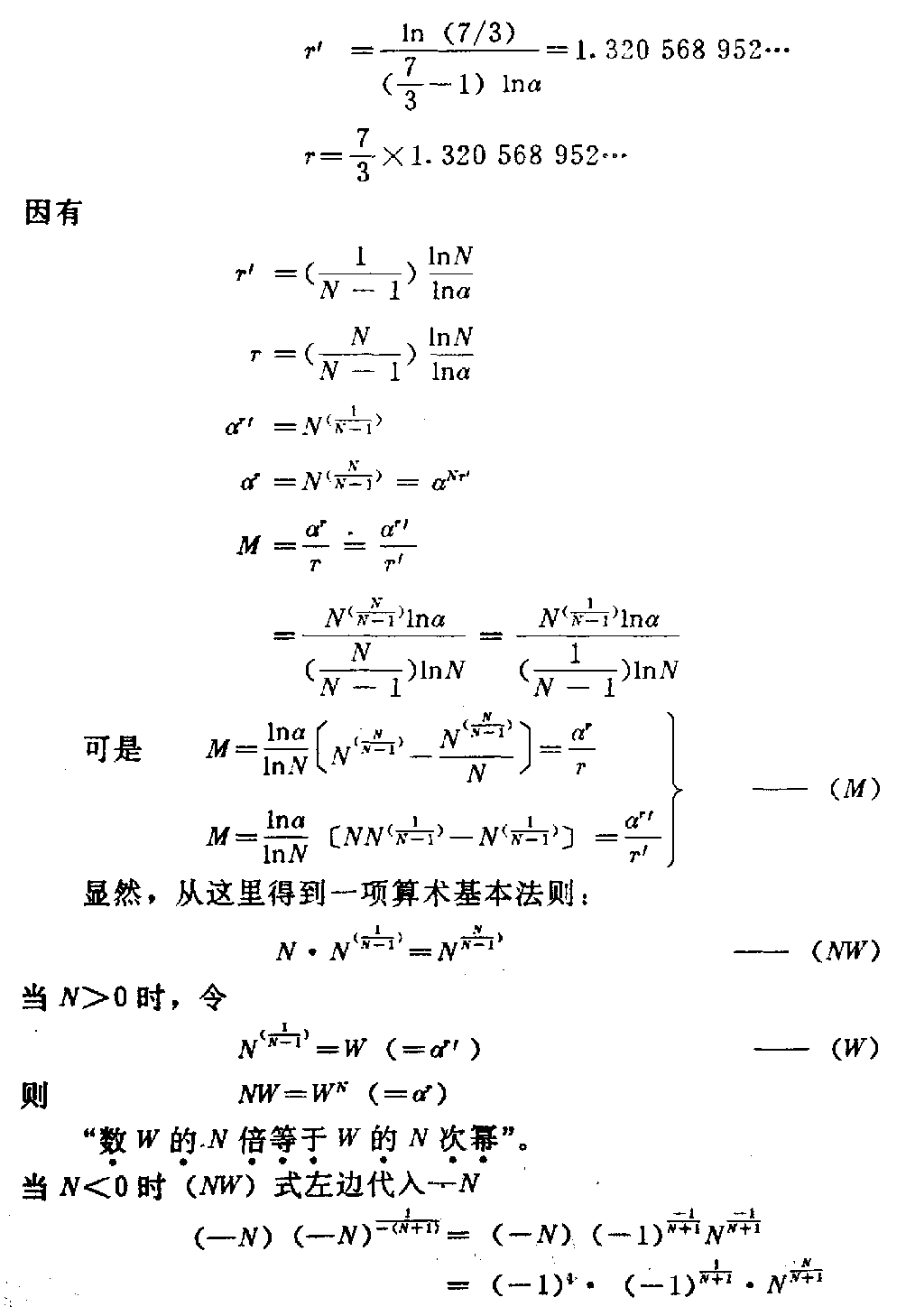
下载——(M) 它由鲁卡斯数衍化而来,但不同于鲁卡斯数。其中 α=12(5+1 ) 式中α的指数r与M中的除数r是同一个数,因此它可以两种形式表示: a.指数形式 r=αrM b.对数形式 r=ln(Mr)lnα a、b两种r式都是M的反函数,因此正函数只有一个(M)式。 1.(M)的反函数之一,a中指数形式的r求值法(指数形式以r’表示) 。 r=αrM 对于这种特殊的隐函数,最好的求值法是无限迭代法。 首先取r0=1,有 r1=αr0M= αM 然后再以r1取r2 r2=αr1M 然后再以r2取r3 r3=αr2M 当令n→∞时,下式成立 limn→∞rn→const 注意,这是某一个M值(一定)时的rn值,当M值改变后,rn则 也变为另一个定值。而每一个rn都是在无限次n的人为代入后产生的。 这种迭代可表示如下 rn=αM αMαMn ∞ 其中,每一个αM都是下一个α的幂指数。 上面两种表示法都很繁琐,我们给了它们一个特定的“函数关系符号” rn=〔αr0→(n-1)M〕∞↑n ——Φ〔Mr0→(n-1)〕 r0→(n-1)为自r0到rn-1, n为人为迭代的次数,趋近于无穷大,每一个rn只对应M的一个数值, 当M≥α时,rn≤1。 r0取为1可以使rn的取得快捷,使r0→rn的中间计 算路程缩短。当然也可以取r0为任意其它正数。 表5列出了M从最小值1400 794 211到13时r′n的数值 ,仅作参考(M≥α,rn≤1)。 表5 M rnMrn1400 794 2111400 794 21180133 299 64α190117 579 08220 7 00 397 10592425926240114 313 15930405 073 81100105 192 28540287 028 80511 0095 169 21950222 614 63 120086 891 64860181 914 1851300799 398 0370153 833 6350595 664 11 3(只取到小数9位) 表中给出几个特殊M值的rn数: (1)M14=1400 794 211…时,r1 4=1400 794 211…, 由此点开始,若M仍为大于1的正整数,可使用“b.对数形式” rn=ln(Mrn)lnα 计算M<1时的r′n,不必用Φ〔M,r′0→(n-1)〕式。当然 也可以继续使用Φ〔M,r′0→(n-1)〕式,令M<1计算r n。由于找到r′1.4=1400 794 211……点,说 明指数形式a与对数形式b是统一的,它们只因M范围不同才有不同形式。 (2)M=5时,r′ 5 =0595 664 113… r′ 5 对于斐波那契数列的应用很有价值,故列入表中。 (3)M=9242 592 624…时,使 r′n=M(=9242 592 624…) 则r′nM=r′2n=αrn(r′n>1) 得r′n1rn =α12 此式在这里仅作说明用。 2.(M)式的反函数之二,b对数形式的r求值法(r不加“”)。 r=ln(Mr)lnα 仍采用无限次迭代法。 首先取r0=1,M为某定值, r1=ln(Mr0) lnα=lnMlnα 再取r2, r2=ln(Mr1) lnα 再取r3, r3=ln(Mr2) lnα 当n→∞时,仍有 limn→∞rn→const 每一个M值的无限次迭代后,都对应一个r值。我们为减少繁琐,也给它一个 特定的函数关系符号 rn=〔lnMr0→(n-1) lnα〕n→∞—— f〔Mr0→(n-1)〕 r0→(n-1)表示r0到rn-1, n为人为迭代的次数,趋近无穷大 每一个rn只对应一个M值, 当M≥α时rn≥1,表6列出 了Mmin=1400 794 211…到M=13时的rn数值(M≥α, rn≥1)。 表6 MrnMrn1400 794 211…1400 794 211 78488 103 412α1888 53 080 48624621 296 312 99171 207 59655028 737 3759242 592 62492 42 592 62436009 853 78610 9453 058 23446892 427 76 9119705 993 52357543 7 94 778129935 344 34768 060 296 0041310145 095 04(只取到小数9位) 由表6中看到 (1)rn≥1(M≥α时) (2)M14=1400 794 211…时, r14=1400 794 211… M14=r14此点在45°分角线上,恰好 Φ〔Mr14〕=f〔Mr14〕 说明此时两条曲线Φ、f在r14=r14点衔接。Φ〔 Mr0→(n-1))在r值≤1400 794 211区域, f〔Mr0→n-1)〕在r值≥1400 794 211区域。 (3)M92=9242 592 624…时, r92=9242 592 624…, M92=r92此点在45°分角线上, 也有r92·M92=r292=αr 92 r1r92 92= α12 此时,可以将Φ〔Mr0→(n -1)〕与f〔Mr0→(n-1)〕两函数按表5、表6数据画出 相互衔接的曲线于坐标roM中(如图17)。 图17 这是一条极特殊的曲线。 3.正函数(M)的求值法及其曲线 如果将(M)式 M=αrr 仍置于Φ〔Mr0→(n-1)〕和f〔M,r0→(n-1)〕 的同一坐标roM中,此时应当是r轴 与M轴调换成Mor。 (M)的求值是正常的,每给定一个r值都对应有一个M值,作0≤r≤+∞ 的M曲线,如图17所示。恰恰(M)曲线与Φf曲线对称于π4角直线。 在这里(M)曲线由一个函数关系作出,不像r=Φ,r=f是两个函数组 成一条曲线。 4.函数(M)及反函数r=f,r=Φ的性质与它们的关系 (1)函数(M)有极小值, M=αrr M′=dMdr,dr dr=1 MM=(lnM)=d dr(lnM) (lnM)=〔lnαrr〕 =〔lnαr-lnr〕=(rlnα)-(lnr) =rlnα-1r 这里r是r的导数,r=dr/dr=1 (lnM)=lnα-1r 极值处的M′=0,故 (lnM)′=0 lnα-1r=0 rmin=1lnα=2078 086 922… Mmin=αrminrmin =1308 069 36… (——rmin仅记为Mmin的r值) rmin与Mmin说明: ①r>rmin或r<rmin时(M)式的M值都增长。当r →0时,M→∞。r→∞时,M→∞。 ②对于r=f(M)与r=Φ(M)以及(M) M<Mmin不存在。 当M>Mmin时,M=αrr=αrr。 这是个极其重要的性质。因此有 rr=αrαr ——(r/r)。 又因Mr=αr,Mr=αr 有rrαr=αr rrnαr=nαr rrnαr±mrrr =nαr±mrrr rr〔nαr±mr〕=nαr±mr rr=nαr±mrnαr ±mr——(r/r) 得到(r/r)0=(r/r)式,指出将式(r/r) 0的分子与分母同时加或减mr与mr,其商不变。其中n、 m为任意实数、虚数,其范围极大。 由(M)式我们看到,M值可以是任何正数,即r值可正(rrmin )。从算术角度出发,只研究正值r、M时,当 r=r=rmin rr=rminr min=1 是比值r/r的最小值。 由于(M)函数是连续、可导的,故比值r/r的运 动区间为 1(r/r)≤+∞ 并可取该区间内的任何数值。 例:取r/r=2,求r,r 同时有αr-r=2 ln2lnα=r-r =2r-r =r 则r=2r=2ln2lnα 于是由(r/r)0式看到,大于1的正数都可以表示为 N=rr=αrα r(1≤N≤+∞) 型的除法关系。 按算术除法规则,我们可以理解型如 rr=r±mr r±mr =r(1±m)r(1±m)=rr 但是,如果写作 rr=r±nαrr ±nαr 时,就“反常”了,我们尚未理解(r/r)0式的来历是难 以置信的,但事实又确是如此,似乎“破坏”了算术除法规则。 关键是r、r并非就是除式表示的m、n。可以任意数 N=mn =rrm≠r,n≠r 但比值相等。 例:如果rr=73,求r,r, 这里r≠7,r≠3。 因rr=αr-r 则r-r=ln(rr )lnα =ln(7/3)lnα 并73r-r=ln(7/3)lnα r=ln(7/3)(73-1 )lnα=1320 568 952… r=73×1320 568 952… 因有 r=(1N-1)lnNlnα r=(NN-1)lnN lnα αr=N(1N-1) αr=N(NN-1)=αNr M=αrr=α rr =N(NN-1)lnα( NN-1)lnN=N (1N-1)lnα(1N- 1)lnN 可是M= lnαlnN N(NN-1) -N(NN-1) N=αrr M=lnαlnN 〔NN(1 N-1)-N(1N-1) 〕=αrr——(M) 显然,从这里得到一项算术基本法则: N·N(1N-1)=NNN-1)——(NW) 当N>0时,令 N(1N-1)=W(=αr )——(W) 则NW=WN(=αr) “数W的N倍等于W的N次幂”。 当N<0时(NW)式左边代入_N (_N)(_N)1-(N+1) = (-N)(-1)-1N+1 N-1N+1 =(-1)1·(-1)1N+1·N NN+1 =(-1)N N+1·NNN+1 (NW)式右边代入_N (-N)-N-(N+1)=(-1) NN+1·NNN+1=(-1)NN+1·WN 故 (NW)式左边=(NW)式右边 由此得到:无论N>0或N<0,数W的N倍都等于数W的N次幂。当N>0 时,NW=WN都是实数,当N<0时,NW=WN等于虚数。 当N=-1时 (-1)NN-1=(-1)12=-1=i (-N)-N-(N+1)=(-1 )12=-1 ——(1) 得到虚数单位i=-1,由这里可以理解(NW)式是 虚数产生的算术根源,数论与复数的关联。当N=lim Δ→1∞(1+Δ)时, (1∞=无穷小) W=N1N-1= lim Δ→0(1+Δ)1Δ =e(纳别尔数) =2.718 281 828 459 045… 当N=limΔ→1∞( 1-Δ)时,(1∞→0=无穷小) W=N1N-1= lim Δ→0(1-Δ)-1Δ =e(纳别尔数) 由此,可理解(NW)式是产生极限 e=limΔ→0(1+Δ) 1Δ 的根源,数论与微积分的关联。 事实上,微积分的基础唯“e”一个极限,是建立在极限“e”上发展起来的 。因为另一个重要极限。 limx→0sim xx=1 中的正弦也是极限e的函数 sinx=eix-e-ix2i(i=-1) 因此,若说微积分是建立在两个重要极上发展的,莫如更确切地说只是极限“ e”的延展与衍化。 当我们到得(NW)、(W)、(M)各式,并在其中含有(m)式、-1、e后,我们就得到了算术是复数、复变函数、微分、积 分的大统一根源的结论。把它们的这些“关系”叫做“关联”有些勉强,从本 文几个式子的由来可见,在一个算术法则中存在着高等数学基本要素,显示了 它的庞大,同时它们不是平行关系,而是根、干、枝的关系。 (2)三条曲线(M)、r=f(M)与r=Φ(M)汇交于两点 r=r=1400 794 211…=M r=M=9242 592 624… 是三个函数的特殊关系点,此时有 M=r=αrr r2=αr r1r =α12 同时有 M=r=αrr r2=αr r1r =α12 得到 r1r= r1r ——(α12) =α12 或2=rlnαlnr= rlnαlnr 由(α12)式,又得到 r1rnn=r′ 1rnn=α 1n ——(α1n) n=rnlnαlnrn =rnlnαlnrn 任意n值的rn、rn求算仍用f(n)、Φ(n)式 rn=lnr0→k1nlnα k→∞=f(n) r′n=αr0→kn ∞↑k=φ(n) 如n=3,4,5,6,7的rn、r′n值列于表7: 表7 nrnrn318029 560 88…12 15 221 43…427569 711 06 …1148 115 22…537718 974 8…1113 073 15…648361 777 65…1091 485 11…759416 72 5 91…1076 835 41… 可以用同法求出更多n的rn、r′n值。 从(α1n)式看到一个奇特的现象 rr′nn=r′rnn rn的r′n次幂等于r′n的rn次幂。 曲线(M)、f(M)、Φ(M)构成的“素数规律”曲线仅是n=2时的型 状,当n→∞时, rn→∞r′n→1 我们注意到 1400 794 211…≥r′(2≤n≤+∞)≥1 就是说,有限区域〔1≤r′n≤1400 794 211…)与无限 区域(+∞≥n≥2〕相对应,但它们都是半封闭的。 通过〔1≤r′n≤1400 794 211…)线段的(M)、f( n)、Φ(n)曲线有(+∞≥n≥2〕多条,每一个n值的函数曲线都有两 点在rn=r′n=M直线上。 所谓“素数规律”曲线只为醒目,实际上,素数规律仅存在于n=2时的r n部分曲线上,且尚未减去(1+α-r)/r,并不是很明显的。 5.由于(α12)、(α1 n)式,我们还可以将“素数规律”的(m)式表达为(α1n)形式: r1rnn=α1 n 则rnn=αrn 有r(n-1)n=αrnrn显然r(n-1)n=M =m+Δ 因而rnn=αrn =rnm+rnΔ =(rnm+1)+(rnΔ-1) 其中rnm+1=αrn-α-rn =rnn-r-nn m=r(n-1)n-r-(n+1)n -r-1n n=rnlnαlnrn——(m,n) 同样,使m为正整数的奇数rn必为素数(rn≥3),否则,rn合 数。 例:设rn=7,求n后代入(m,n)式 有n=7lnαln7=1731 05 7 714… m=7(n-1)-7-(n+1)-7 -1 =4 rn=7是素数 显示了“r数”的作用。 我们从双曲函数关系中知道,实数都可表示成(虚数另式) 公式r=cosh(lnr)+sinh(lnr) 德·莫弗公式=〔cosh(1)+sinh(1)〕 lnr =elnr 故e=r1lnr 两边的lnαr次幂 elnαr=r(lnαr lnr) 因n=lnαrlnr elnαr=αr, 也得αr=rn 即(α1n)式。 由已知的双曲函数证得(α1n)式,仅此而已 ,单纯的数学关系推导,尤其不能表现r的存在,毫无新的数学意义。 (m)式也可表示成为双曲函数形式,其中 αr-α-r=2sinh(lnαr) 则m=2sinh(lnαr)-1r 6鲁卡斯数列Ln的两个形态 Ln=αn+(-1)nα-n 若令α-1=β,n为偶数与n为奇数的Ln可同时写为 Ln=αn±βn 因α=5+12,β= 5-12 则Ln=〔5+12〕n±〔5-12〕 n 2n=αn2nαn±βn±βn2nαn±βn 得 1=11+β2n+ 1α2n+1 1=11-β2n-1α 2n-1——(u) 我们又获得两个同类更为广义的斐波那契数列封闭式,推演过程消除了2n ,所以知道鲁卡斯数列仅是关于2n的一种(u)式,因此可以(u)式随意 发展。 7.鲁卡斯数与斐波那契数的一个简单关系 除了Fn=15L (n-) 外,还找到整数系数关系。 L(n-)=αn-(-1)nα-n 鲁卡斯数Ln=αn+(-1)nα-n, α=12(5+1), n≥2时 有L1=1,L2=3,Ln=Ln-2+Ln-1 递推关系。 我们注意到 L3=(L1+L2)+0×L2 L4=L2+L3=L2+(L1+L2) L5=L3+L4=2(L1+L2)+L2 L6=L4+L5=3(L1+L2)+2L2 L7=L5+L6=5(L1+L2)+3L2 L8=L6+L7=8(L1+L2)+5L2 …… L13=L11+L12=89(L1+L2)+5 5L2 L14=L12+L13=144(L1+L2)+ 89L2 即Ln=Fn-2(L1+L2)+F n-3 L2 Ln=4Fn-2+3Fn-3—— (Ln=Fn-2,3)
